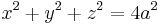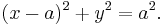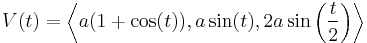Viviani's curve

In mathematics, particularly geometry, Viviani's curve, also known as Viviani's window, is a space curve named after the Italian mathematician Vincenzo Viviani, the intersection of a sphere with a cylinder that is tangent to the sphere and passes through the center of the sphere.

Formula

The curve can be obtained by intersecting the unit sphere of radius 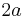$2a$ given by

$x^2%2By^2%2Bz^2=4a^2 \,$

with the cylinder centered at 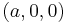$(a,0,0)$ of radius $a$ given by

$(x-a)^2%2By^2=a^2. \,$

The resulting curve of intersection, $V$ , can be parameterized by $t$ to give the parametric equation of Viviani's curve:

$V(t)= \left\langle a( 1%2B\cos(t) ), a\sin(t), 2a\sin\left(\frac{t}{2}\right) \right\rangle$

See also

Sphere-cylinder intersection

External links

Weisstein, Eric W., "Viviani's Curve" from MathWorld.